게이지 통해 옷 치수 계산할 때
수학적 감각 자연스레 길러져
입체도형 이해력도 높일 수 있어
뫼비우스의 띠 설명에 사용되기도
절기상 첫 눈이 내린다는 소설(小雪)이 지나기 무섭게 첫 눈 소식이 들려 오니, 새삼 겨울의 문턱에 다다랐다는 것을 실감하게 됩니다. 또 한 가지, 주변 여기저기서 털실 뭉치와 바늘을 들고 뜨개질하는 모습도 겨울철의 익숙한 풍경입니다.
뜨개질은 겉보기에는 자칫 단조롭고 지루한 활동처럼 보일 수 있지만, 실제로는 손은 물론 머리도 많이 써야 하는 활동입니다. 두 개의 바늘만으로 무궁무진한 작품을 만들 수 있어, 누군가는 뜨개질을 ‘두뇌 스포츠’라고 말하기도 합니다. 그 속에 수학 원리가 숨어 있기 때문인데, 어떤 것들이 있는지 들여다볼까요.
뜨개질을 시작하기 전 가장 먼저 해야 하는 것이 ‘게이지’ 측정입니다. 게이지란 일정한 면적 안에 들어가는 코와 단의 수를 뜻합니다. 자신이 뜨려고 하는 뜨개질법과 실로 사방 15cm 정도의 샘플 조각을 떠본 후 ‘얼마만한 치수의 옷을 뜰 때 몇 코, 몇 단을 뜰지’를 가늠하는 것으로, 완성품의 치수를 정확하게 맞추기 위해 매우 중요한 과정입니다. 실의 종류, 바늘의 굵기, 뜨는 사람이 힘을 얼마나 주는지 등에 따라 뜨개질의 결과물이 달라지므로 게이지 측정을 정확히 해야 하는 것이지요.
사방 15㎝의 샘플 조각을 뜬 다음 가장 고르게 떠진 사방 10㎝ 안의 콧수, 단수를 세어 봅시다. 이를 각각 10으로 나누면 1㎝에 코와 단이 각각 몇 개씩 들어가는지 계산할 수 있습니다.
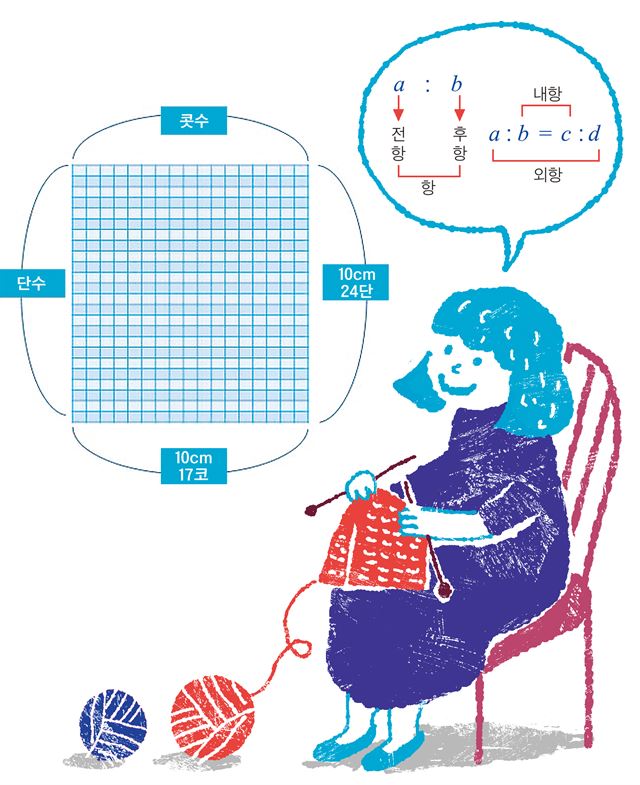
<그림1>은 게이지 계산을 이해하기 쉽게 표현한 것입니다. 사방 10cm의 샘플을 뜬 후 코와 단의 수를 세어보니 17코, 24단이 들어가는 것을 확인할 수 있습니다. 즉, 1㎝ 정사각형 안에는 각각 1.7코, 2.4단이 들어가는 셈이 되는 것이지요.
게이지를 통해 옷 치수를 계산할 때에는 비례식이 사용됩니다. 완성할 옷의 뒤품이 43㎝일 때, 필요한 콧수는 ‘1 : 1.7 = 43 : x’라는 식을 세워 계산할 수 있습니다. 1㎝에는 1.7코가 필요하니, 43㎝에는 몇 코가 필요할지를 수식화한 것입니다. x값은 내항의 곱과 외항의 곱이 같은 비례식의 성질을 이용해 계산하면 됩니다. x=1.7x43을 계산하면 x값은 73.1이 나옵니다. 즉, 계산을 통해 뒤품이 43㎝인 옷을 만들 때에는 73.1을 반올림한, 73코가 필요하다는 결과를 얻게 됩니다.
몇 단이 필요한지도 계산해 볼까요? 옷의 길이가 65㎝일 때, 필요한 단수를 구하는 식은 ‘1 : 2.4 = 65 : y’ 입니다. 비례식의 성질에 따라 계산을 해보면 y=2.4x65 즉, 길이가 65㎝인 옷을 만드는 데는 156단이 필요한 것을 알 수 있습니다.
나아가 뜨개질은 패턴을 통해 규칙성을 익히기에도 좋은 소재입니다. 뜨개질법에 따라 다르게 표현되는 패턴의 형태를 인식하고, 콧수와 단수에 따라 패턴이 어떻게 반복되는지를 살펴 보면 규칙을 이해하는 수학적 감각을 기르는 데 도움이 됩니다. 뜨개질처럼 주변에서 쉽게 접할 수 있는 소재를 통해 자연스럽게 길러진 수학적 감각은 수의 규칙성을 배울 때에도 든든한 밑거름이 될 수 있습니다.
또한 뜨개질로 작품을 만들다 보면 도형의 기본 요소인 선과 면을 직관적으로 이해할 수 있으며, 원, 삼각형, 사각형 등 평면도형은 물론 입체도형에 대한 이해력도 높아집니다. 실제로 수학자 사라 마리 벨캐스트로는 뜨개질의 수학적 요소를 간파하고, 수학 개념을 뜨개질에 이용하거나 뜨개질을 통해 수학 개념을 설명하기도 했습니다. 기하학적 패턴과 수학적 규칙을 이용해 뫼비우스의 띠, 클라인의 병, 쌍곡면, 매듭 등을 만든 것이지요.

실과 바늘만으로 구상한 작품을 만들어내는 과정은 가히 무(無)에서 유(有)를 창조하는 것과 견줄만합니다. 이 때, 무심코 했던 뜨개질 속에도 수학 원리가 있음을 알고 나면 작품을 완성했을 때의 뿌듯함도 배가 되지 않을까요. 올 겨울엔 손수 뜬 뜨개 작품을 친구나 가족에게 선물하고 감사의 마음을 전하는 것도 좋겠습니다.
[스토리 플러스]
양 끝이 이어진 매듭을 분류하고, 이들의 특성을 연구하는 수학 이론을 ‘매듭이론’이라고 합니다. 매듭이론은 복잡한 함수를 뜨개질 모델로 만든 스코틀랜드의 화학자 알렉산더 크럼 브라운과, ‘분자의 화학적 성질은 이를 구성하는 원자들이 어떻게 꼬여서 매듭을 이루고 있는가에 달려 있다’는 켈빈의 ‘볼텍스 이론’을 토대로 연구되고 있습니다. 오늘날 매듭은 DNA 구조나 바이러스의 행동방식을 연구하는 데 중요하게 사용되는 등 연구가치가 높아 주목 받고 있습니다.
[문제 연습하기]
대동여지도는 조선 후기 지리학자인 김정호가 만든 우리나라 목판 지도로, 조선시대에 만들어진 가장 정확하고 정밀한 최고의 과학적 실측지도로 높이 평가 받고 있습니다. 대동여지도는 크기가 가로 3m, 세로 7m나 되고 축척(실제 거리를 도면상에 축소시킨 비율을 나타낸 것)은 약 1 : 160,000인 거대한 지도랍니다.
문제: 지금의 서울은 한강을 사이에 두고 남북으로 펼쳐져 있고 동쪽과 서쪽 사이의 거리는 약 36 km입니다. 서울의 동쪽과 서쪽 사이의 거리는 대동여지도에서 몇 ㎝로 나타나 있겠는지 풀이 과정을 쓰고 답을 구하세요.
정답: 22.5㎝
풀이: 예) 36㎞ = 3,600,000㎝이고 대동여지도에서의 거리를 □㎝라 하면
1 : 160,000 = □ : 3,600,000
1x3,600,000=160,000x□, □=3,600,000÷160,000
□=22.5
따라서 대동여지도에서 22.5㎝로 나타나 있습니다.
<출처: 천재교육 ‘스토리텔링 해법수학 6-2’>
기사 URL이 복사되었습니다.

댓글0